A Pythagorean triplet is a set of three natural numbers, a
a2 + b2 = c2
For example, 32 + 42 = 9 + 16 = 25 = 52.There exists exactly one Pythagorean triplet for which a + b + c = 1000.
Find the product abc.
Solution:
As usual, there is not only one correct way to solve this problem. The most obvious solution is to test every possible combination of a,b,c up to a specified limit and verifying that the combination fulfills both requirements. However, I decided to utilize Euclid's Formula for finding triplets. According to wikipedia:
Euclid's formula[1] is a fundamental formula for generating Pythagorean triples given an arbitrary pair of positive integers m and n with m > n. The formula states that the integers
form a Pythagorean triple.
These equations can be used to solve this problem. Since we want
a + b + c = 1000
We substitute in the paramaterizations in terms of m and n.
m2 - n2 + 2mn + m2 + n2 = 1000
=2m2 + 2mn = 1000
=m2 + mn = 500
mn = 500 - m2
n = (500 - m2) / m
We know that we are looking for integer values of n, so if the equation yields a remainder we know that we can just skip the rest of the loop and try the next value of m.
One other little tidbit to recognize is that we are only intested in positive values for a, b, and c. Since the equation
b = 2mn
produces a negative result for a when n or m < 0, and since we are solving n in terms of m, we really just need to find out for what values of m will produce a negative n. To solve, we substitute 0 for n in the equation
n = (500 - m2) / m
0 = (500 - m2) / m
By inspection, we can see that n will be negative when |m| > sqrt(500) or approximately +/-22.36. This means that for certain, m will be less than or equal to 22.
Now lets look at the equation for a:
a = m2 - n2
Obviously, this produces a negative number when n > m. This tells us that we should start at the maximum value for m and decrement it with every iteration until n > m. If we reach the point where n > m and a solution has not been found, then no solution exists.
To test whether a given value of m and corresponding n produce the correct a, b, c for our equation, we simply check whether
a2 + b2 = c2
(note: This particular problem can be solved by skipping this last step since our target number of 1000 is small. However, I believe that as this number gets larger this step is required... if you have insight to this I would love to hear it.)
What all this means is that rather than using nested loops and going through every value for a, b, and c, all we need is ONE loop and to go through a handful of values of m! Namely,
n < m <= 22
Finally, if (a,b,c) is indeed the pythagorean triple we seek, we break out of the loop and find their product.
So here it is...
#include <stdio.h>
#define target 1000
int main (void)
{
int a = 0, b = 0,c = 0,n = 0, m = 22;
int tar = target / 2;
int found = 0;
while (!found)
{
int divides = ( tar - m*m ) % m;
if (!divides) // If there is no remainder
{
int a_sqr, b_sqr, c_sqr;
n = ( tar - m*m ) / m ;
if ( m < n )
{
printf("No solution was found.\n");
break;
}
a = m*m - n*n;
b = 2*m*n;
c = m*m + n*n;
a_sqr = a * a;
b_sqr = b * b;
c_sqr = c * c;
if ( (a_sqr + b_sqr) == c_sqr )
found = 1;
}
m--;
}
printf("a = %d, b = %d, c = %d\n", a, b, c);
printf("abc = %d", a*b*c);
return 1;
}
Compile and watch the answer appear before your eyes!
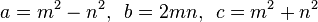
No comments:
Post a Comment